[最適化問題のすゝめ：第2部] 数理最適化の問題を解いて理解を深めよう

2021.04.30
技術記事

みなさんは数理最適化や最適化問題ということばをご存知でしょうか。
おそらく「最適化ということばは、よく聞くけれど詳しくはしらない」という方が多いのではないかと思います。

数理最適化という道具を用いて作成する問題を最適化問題と呼びます。最適化問題は、考えないといけない制約が複数ある状態で、ある目的を最大・最小にしたいオーダがある際に役立ちます。実際に具体例を挙げてみます。

  • コンビニへ商品配送におけるルート最適化問題
  • カーナビのルート探索
  • 工場の製品機器への割り当て問題
  • 病院で働く看護時のシフト勤務問題

想像していたより実社会における適用範囲が広いと感じたのではないでしょうか。
今回は、数理最適化のことをより深く知っていただけるように、２部構成の記事を組みました。

第一部では数理最適化の特徴や種類のお話、最適化と密接に関係してくるソルバのお話をしたあと、有名な「どろぼうの問題（ナップザック問題）」を通して最適化への理解を深めることができる流れになっています。

第二部目では第一部にて学んだ内容を踏襲しつつ、著者が作成したオリジナル問題を通してより汎用的な最適化問題を解き、興味・理解を深めていただければと思っています。

第一部をまだご覧になっていない方は以下からごらんください。

前回記事：「[最適化問題のすゝめ：第1部]数理最適化とは？種類や特徴を解説」

オリジナル問題を作成してみる

ここからは第一部で学んだことを思い出しつつ、著者が作成したオリジナル問題を用いて最適化問題についてより深く学んでいきましょう。最適化問題を解く構成は、おおまかに「定式化→モデリング→最適化計算→解分析」の流れになっていると第一部で話しましたね。しかし、有用な最適化問題を構成するためには、パラメータ調整や新たな制約追加・削除を何度か繰り返し行う必要性もあります。

ではどうすればいいかと言いますと、そのようなパラメータ調整自体をユーザ自身にコントロールしてもらえるように仕様を構成するというのはどうでしょうか。このような方法も一つの手ではないかと考えています。著者は、後ほど説明するオリジナル最適化問題にて、Streamlitと呼ばれるフロントエンドアプリを作成できるpythonのフレームワークを用いて、ユーザ自身にパラメータを調整してもらう仕様にしました。さらに入力データ内容や出力結果も目視してもらえるようにしました。そうすることで、ユーザの手元でいろいろなパラメータ値で試した結果を目で見てもらえるという利点があります。

シフトスケジューリング問題

ここからは著者が考えたシフトスケジュール問題について説明します。では、シフトスケジューリング問題の設定をみていきましょう。

問題：
データサイエンス課にいるメンバーたちは、ある出店を1週間出店することになりました。そのため、メンバーのシフトを決める必要がでできました。メンバーには平等でいて欲しいため、シフト希望日が採用される回数の隔たりが、なるべく少なくすむようにしたいです。それぞれのメンバーには、予めエクセルシートにシフト希望日の入力をしてもらうこととします。ただし、考慮したい項目として下記のような内容があります。
(い)：毎日、PGM（プログラムマネージャ）が1人も出勤しないと困るので、出勤の下限の人数を決めたい。
(ろ)：平日、出勤する人数の下限・上限を自由に決めたい
(は)：土日は、忙しいことが見込まれるため下限人数を決めたい。

定式化の作業にうつる前、まずは最適化問題フレームワークを構成する上で、使用する環境の方針や前提条件を決めておきましょう。

  • 使用する環境の方針
    • 本問題では、解出力形式の都合上「②APIを利用してソルバ計算」を採用することしました。
    • モデリングにはPythonモジュールであるpulpを使用し、ソルバは無償提供されているGLPKを使用します。
    • Streamlitと呼ばれるフロントエンドアプリを用いて、最適化問題を構成する制約のパラメータ値をユーザ入力から受け付けることとします。
  • 前提条件
    • 最適化問題のパラメータ情報として、メンバーが予め一週間の曜日ごとのシフト希望を記入したcsv/Excelファイルがあるものとする。
    • シフト希望内容をファイルに記入する場合、働ける曜日に1、働けない曜日に0と記入すること。

定式化

上記の問題文から定式化を行います。問題を定式化すると下記のようになります。問題文と照らし合わせてみてください。

シフトスケジューリング問題の定理化

制約条件(2.1)~(2.3)は、平日シフトの出勤人数の上下限、土日シフトの出勤人数の下限、毎日のシフトに必要なPGMの下限人数を設定する制約です。それぞれの制約の上下限値をパラメータとして定義しています。こうすることで、ユーザ入力から受け付けた内容を反映させる狙いがあります。また、それぞれの制約は、問題文にかかれている考慮したい事項の(い)~(は)の要望に対応しており、メンバiがj曜日に働くとき1,働かないなら0を意味する0-1変数であるxijと集合の要素をうまく利用して式を表現しています。

制約条件(2.4)は、シフト希望採用回数の上限・下限を設定する制約です。メンバはシフト提出時に働くことができる曜日を提出しています。実際にシフトに入る（働く）ことが決定した曜日の日数に応じてxijが変化します。例えば、メンバの1人であるAyakaが一週間のシフトで月曜日と火曜日のみ働くなら ∑ i∈I x Ayaka Mon = 1, x Ayaka Tue = 1 となり、 ∑ i∈I x ij = 2 となります。つまり ∑ i∈I x ij を変数u, lで挟むことでシフト希望採用回数の上下限を得ることができる仕組みです。

制約条件(2.5)は、シフト希望日以外の出勤を禁止する制約です。予め提出したシフト上で働けない曜日として提出しているにも関わらず、最適化計算後に働くことになっていては困りますよね。そのような事態をさけることができるように制約を設定する必要があります。制約にでてくる(sij  xij)の組合せは、(1 1),(1 0), (0 1), (0 0)の4つあります。この4つの中から「シフト希望で入れない日（つまりsij=0）として提出したのに、実際働くことになった（つまりxij=1）」場合を除けば都合が良くなります。つまり、sij-xij ≥ 0と設定することで、(sij  xij)= (0 1)の場合を除く制約にすることができますね。

制約条件の(2.6)は、「どろぼうの問題」でもでてきた通りxijが0-1変数であるという意味を示す制約です。

最後に目的関数です。目的関数は制約条件(2.4)で設定された変数u, lの差分を最小にする制約です。問題文にかかれている「メンバーには平等でいて欲しいため、シフト希望回数が通る回数の隔たりがなるべく少なくすむようにしたい」という要望に対する内容です。一般的に隔たりをなくす（いわゆる平準化）場合、最大値の最小化もしくは最小値の最大化などいろいろなアプローチがありますが、今回は最大値と最小値の差分を最小にすることで平準化を実現することにしました。

モデリング

「②APIを利用してソルバ計算」を採用した場合における、モデリングを見てみましょう。まずは記号を定義した部分です。

# シフト情報の読み込み
df_in = pd.read_csv("../input_data/提出済みDSシフトスケジュール問題.csv", index_col=0)

# 最適化問題の宣言
m = LpProblem("DS_Shift-ScheduleProb")

#### 集合
# 人の集合
I = df_in.index.values.tolist()
# PGMの集合
I_ = I[8:11]
# 曜日の集合
J = df_in.columns.tolist()
# 祝日の集合
J_ = J[5:7]
#### パラメータ
# 提出したシフト
shift = df_in.values.tolist()
s = {} # 空の辞書
for i in I:
    for j in J:
        s[i, j] = shift[I.index(i)][J.index(j)]

#### 変数
up = LpVariable("u", lowBound=0)
low  = LpVariable("l", lowBound=0)
x = {}
for i in I:
    for j in J:
        x[i, j] = LpVariable(f"x({i},{j})", cat=LpBinary)

この部分では、提出されたシフト情報を読み込み集合やパラメータ値を設定しています。前提条件で決めたように提出済みのシフトにはメンバーの希望情報が0か1で記入されています。上記の提出済みシフト情報をpythonのデータフレームとして取得し、メンバと曜日の要素を読み込みます。さらに得られたメンバのうちPGMメンバを指定し、曜日も同様にして土日の設定を行っています。また、どのメンバーがどの曜日に働く・働かないのかという情報を辞書データとして取得していることがわかります。

次に定式化の部分です。

#### 目的関数
        m += (up - low)
#### 制約条件
st.header('▼ 作成するシフトの設定')
# 出勤人数の上限
LB_shift = st.slider(
    '① 出勤人数の下限を決めてください', min_value=0, max_value=10, step=1, value=1)
st.write("→ 毎日、少なくとも", LB_shift, '人は出勤します。')

# 出勤人数の下限
UB_shift = st.slider(
    '② 出勤人数の上限を決めてください', min_value=0, max_value=10, step=1, value=4)
st.write("→ 毎日、多くても", UB_shift, '人まで出勤します。')
for j in J:
    # １日少なくとも*人は出勤、多くても*人まで
    m += lpSum(x[i, j] for i in I) >= LB_shift, f"LB_shift_{j}"
    m += lpSum(x[i, j] for i in I) <= UB_shift, f"UB_shift_{j}"

# PGMは少なくとも1人毎日出勤する
UB_PGM_shift = st.slider(
    '③ PGMの下限を決めてください', min_value=0, max_value=2, step=1, value=1)
st.write("→ 毎日、少なくとも", UB_PGM_shift, '人はPGMが出勤します。')
for j in J:
    m += lpSum(x[i, j] for i in I_) >= UB_PGM_shift,  f"PGM_shift_commit_{j}"
# 土日の出勤人数の下限
LB_sunsat_shift = st.slider(
    '④ 土曜日・日曜日の出勤人数の下限を決めてください', min_value=LB_shift, max_value=UB_shift, step=1, value=3)
st.write("→ 土日は、少なくても", LB_sunsat_shift, '人は出勤します。')
# 土日は*人以上出勤する
for j in J_ :
    m += lpSum(x[i, j] for i in I) >= LB_sunsat_shift,  f"LB_shift_SunSat_{j}"

##### その他の制約
# シフト希望が通る回数の下限と上限
for i in I:
    m += lpSum(x[i, j] for j in J) >= low  , f"LB_Staff_Satisfy_{i}"
    m += lpSum(x[i, j] for j in J) <= up  ,   f"UB_Staff_Satisfy_{i}"

# シフト希望日以外は出勤しない
for i in I:
    for j in J:
        m += s[i, j] >= x[i, j],  f"Shift_({i}{j})"

「どろぼうの問題」と違うポイントとしては、変数の添え字が変化したことでしょう。添え字が1つから2つになっているため、Pythonコード中のforループが2重になっている箇所があることがわかりますね。また、Streamlitを使用して、ユーザ入力から受け付けたパラメータ情報を制約条件の内容として反映するような書き方になっていることも、ポイントになっています。このように記号の定義、制約条件と目的関数の設定を行うことでモデリングが完成しました。

インターフェース

では、実際にどのようなインターフェースでユーザからの入力受付がおこなわれるのかを少しお見せします。それぞれのパラメータ値をスライダーで調整できるようになっています。そしてユーザが設定したスライダーの値から最終的に採用する値を再確認している様子がわかります。

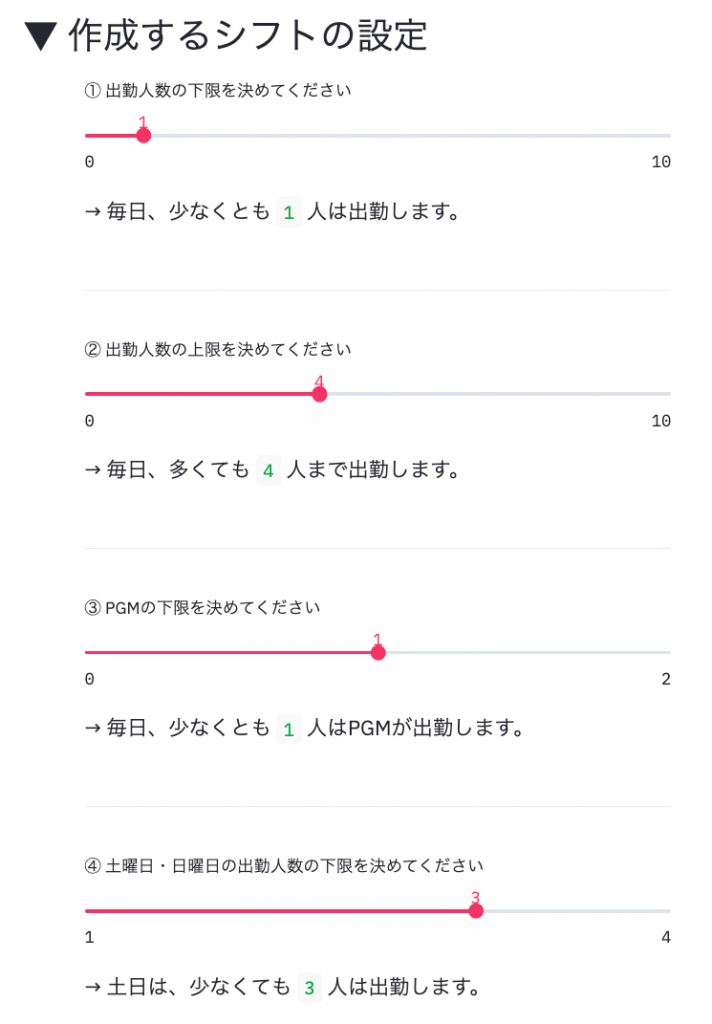
シフト制作のインターフェース、スライダー設定

上記の設定が終了すれば、最適化計算をスタートできます。「最適化計算スタート」ボタンを押せば、裏で最適化計算がまわりはじめます。

シフト制作のインターフェース、最適化を計算

解がみつかれば、結果が出力されてユーザは目視して確認することができます。

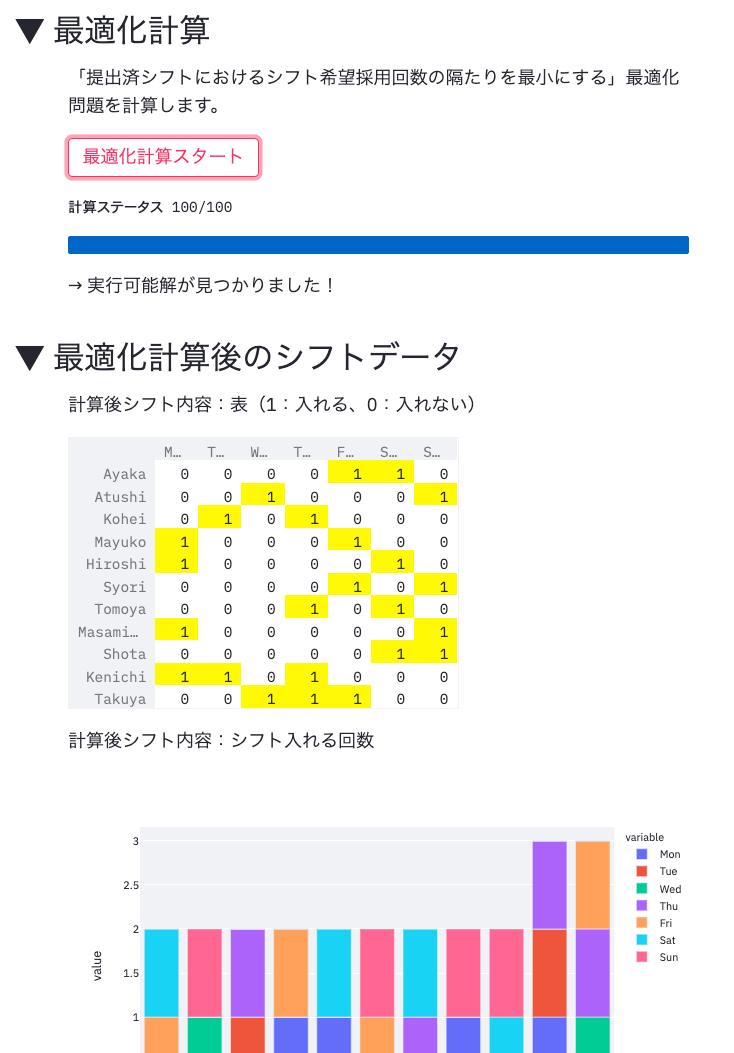
シフト制作のインターフェース、最適化計算結果を表示

最適化計算後の出力

最後に最適化計算後の出力についてお話しします。出力までの過程は以下のイメージのようになっています。

最適化計算後の出力出力までの過程

入力内容である提出済みのシフト希望のデータと最適化問題の構成に必要なユーザからの入力情報を利用して最適化計算を行います。計算後に、どのメンバがどの曜日に働くかどうかの情報を計算後の変数値を利用すれば、うまく取得できるはずですね（0と1のデータで表現されています）。

まずは、取得できた情報を一時的な出力としてテキストファイルに書き出します。さらに、そのテキストファイルの内容を用いて、あらかじめメンバと曜日が書かれた中身の埋まっていないデータの中身の値を埋める作業を行っています。このような命令を下記Pythonコードで表現しています。

# 書き込み設定
if m.status == 1:
    st.markdown("→ 実行可能解が見つかりました！")
    # 計算結果 → テキストファイル
    with open("../output_data/result_ShftSchedule.txt", "a", newline="") as file:
        for i in I:
            for j in J:
                print(x[i,j].value(), file=file, end="\n")

# テキストファイルのデータ → エクセル
    book = openpyxl.load_workbook('../output_data/result_ShftSchedule.xlsx', data_only = False)
    sheet = book['result']
    file_data = open("../output_data/result_ShftSchedule.txt", "r", encoding="utf-8")
    # 指定箇所から書き込み
    for j in range(2, 13):
        for i in range(2, 9):
            pattern_data = file_data.readline().rstrip()
            # エラー処理（ファイルが空の場合はskipする）
            try:
                sheet.cell(row=j, column=i).value = str(pattern_data)
            except :
                continue

        # ファイル出力
        filename, file_extension = os.path.splitext("../output_data/result_ShftSchedule.txt")
        out_file =  filename + ".xlsx"
        book.save(out_file)

おわりに

いかがでしょか、最適化問題について少し興味がわいてきたでしょうか。ここまでの内容を通して、様々なことを簡単にですが説明してきました。加えて、忘れてはいけないこととして、最終的に出力されて結果が本当に正しいかどうかを確認する作業があります。つまり正しく制約が機能しているかどうかを確かめる作業になります。確かめるべきポイントとして何点か挙げてみました。

  • 提出したシフトで0（出勤できない）と指定したのに1（働く）になっていないか
  • 毎日、本当にPGMが指定した下限人数いるかどうか
  • コンソール出力内容とStreamilt出力内容が合致しているかどうか 

例えば「提出したシフトで0（出勤できない）と指定したのに1（働く）になっていないか」の確認はstreamlit上で表示される内容を見比べてみればわかりますね。その他のことは、公開リポジトリに同じ環境を準備してますので、ぜひご自身の手で確かめてみてください。

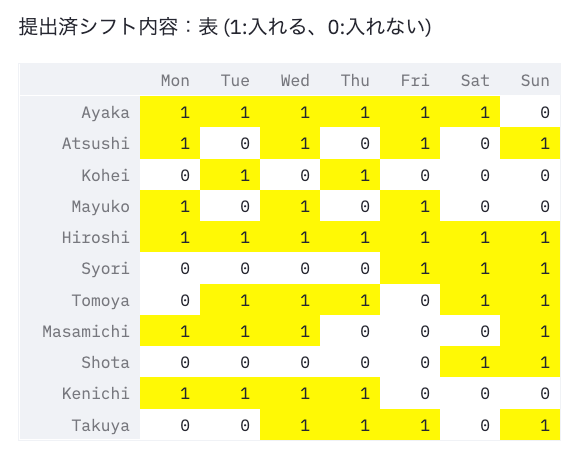
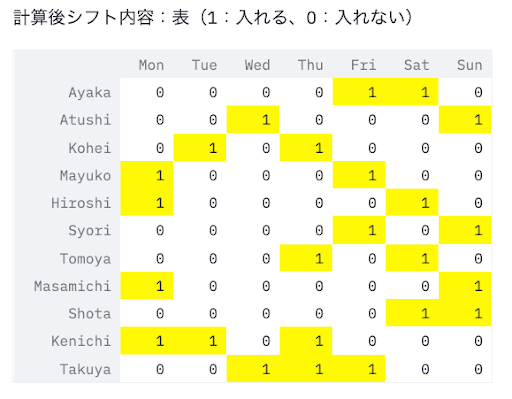
計算後のシフト内容
計算後のシフト内容

最後になりますが、ポイントをまとめて記事を締めさせていただけきます。

  • 一般的に数理最適化問題には１つの目的関数と複数の制約条件で構成されている。
    • 最適化問題では、複数制約下で一番よい状態となる目的関数の値を算出する
  • 数理最適化問題を解く際には、ソルバと呼ばれるアプリケーションを使用することで、効率よく解を得ることができる。
  • 計算結果の出力までの道のりは主に2パターン
    • ① モデリング言語AMPLを用いてモデリングし、CUIを利用してソルバ呼び出しを行い最適化計算、解の算出を行う。
    • ② API（Python言語）を利用してモデリングからソルバ計算と解の算出を行う。
  • ②を利用すれば、Streamlitなどのインターフェースと連携することができる。
  • 解の検証（意図した通りに制約条件がうまく効いているがどうか）は忘れずに…

執筆者：山本

この記事を読んだ方におすすめ

Contact

お問い合わせはこちら

詳細資料、無料相談、お見積もり、ご依頼などお気軽にお問い合わせください

お問い合わせ