[最適化問題のすゝめ:第1部]と[最適化問題のすゝめ:第2部]の記事は既にご覧いただけましたでしょうか。想像していたより実社会における適用範囲が広いのではないかという可能性を感じていただけたと思います。
一般的に数理最適化問題を作成し、問題解決に至るまでは以下のようなステップを踏むことが理想となります。一番最後のステップまで行くと最初に戻り、繰り返すことで、よりよく社会へと馴染む最適化問題へと変化することが可能です。
- 現実問題の情報整理・収集する
- 数式などを用いて定式化する
- アプリケーションやモジュールを用いてシステム化する
- 計算結果から問題点や追加要素を見出す
今回は上記4つのうち、1つ目の「現実問題の情報整理・収集する」に着目し、著者が個人的に好きなスケジュール問題に絡めて説明することにします(他3つについては別記事「[最適化問題のすゝめ:第1部] 数理最適化とは?種類や特徴を解説 」や「第2部] 数理最適化の問題を解いて理解を深めよう 」にて説明しています)。
本記事を通して、モデル化や定式化までの道のりの第一歩となる現実問題の情報整理・収集をどのようにしていば良いかを知ってもらえれば幸いです。
スケジューリング問題
みなさんは、そもそもスケジューリング問題にどのようなものがあるかご存知でしょうか。
- 旅行スケジューリング
- シフトスケジューリング
- 電車運行スケジューリング
- 生産スケジューリング
- 時間割表作成スケジューリング
ご覧の通り、対象となる主人公にはヒトや機械などさまざまです。
以下では、このうちのいくつかをピックアップしてどのようなものがあるか、詳しく紹介します。
シフトスケジューリング
シフトスケジューリングは、一定期間のシフトを作成する問題のことをいいます。
数理最適化業界ではよく割当問題(月曜X時に一人シフトを割り当てするという意味で割当という単語をつかって表現する)と呼ばれることもあります。
ここで目的とされることは、以下のようなものがあります。
- 残業費用(人件費)の最小化
- 製品納期に向けた計画立案(予定日からの差分最小化)
- 機械 or ヒトの生産数最大化
- 品質目標を満たすための生産性の最大化
また、目的関数を設けず、組合せ(人員とシフト)を探すためだけに用いることも可能です。ただし、問題を考える際の注意点があり、例えば以下が考えられます。
- 法律の定める労働時間等に違反していないか
- 体調面を考えて連勤しすぎていないか
- 休憩時間を加味した勤務表にするのか
- 人員同士の相性や教育の観点での組み合わせに問題ないか
ナーススケジューリング
ナース スケジューリング問題はシフトスケジュール問題の一部として割り当てられる場合もありますが、このジャンルにおいて盛んに研究されているテーマの一つです。
ポイントとしては、特に患者さん・生命に関わるお仕事なので、人数、人員同士の相性や人員の健康状態などといった制約は特に気にする必要があるというところです。
- 特徴
- ナーススケジューリング問題(nurse scheduling problem, NSP)と呼ばれます
- 多くのNSPは組合せ最適化問題として定式化されます
- 考慮すべき制約の種類が多いため解くことが困難(時間内に計算が終わらない、解が一意に定まらない)であることがあります
- 歴史
- 1990年代の後半には、NSPに関する研究が盛んに行われはじめました
- 昨今、多くの病院では現在も手動でスケジュールを作成し、計算機やコンピュータを用いて勤怠管理やメンバーを管理するために使用されることが多いようです
- ポイント(制約)
- 負担や健康
- 週X回は勤務可能、何時までなら勤務可能、休みは週X回以上ほしいなど、連勤が続き過ぎていないか
- 支障が起きないように構成
- 必要人数の最低ラインは超えているか、スキルレベル的に問題のない構成か、相性は問題ないか
- 負担や健康

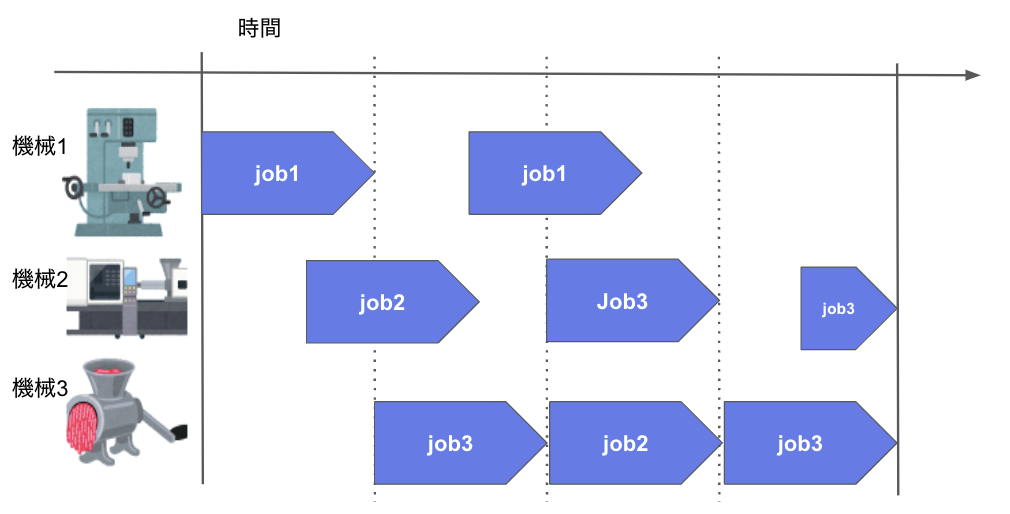
生産スケジューリング
- 特徴
- 工場における資源の計画を策定する問題です
- ある一定期間において、資源を生む機械やその機械の性能を考慮しつつ、納期や生産量を満たすためのスケジュールを考える問題です
- ある一定の生産量を満たすために、順序などの組み合わせを考えるパターンもあります
- ポイント(制約)
- 機械の連続稼働時間は問題ないか
- 加工時間は加味されているか
- 製造の順序は考えなくていいのか
- 性能として一定期間にどれくらい生産することができるのか
- 一日どれくらいの量以上生産すれば最終目標に間に合うのか
現実問題の情報整理・収集する
それでは、ここからは本記事の本題である「現実問題の情報整理・収集」をどのようにすれば良いかについて紹介していきます。
要素の整理
まずはどのような問題になりそうなのかを下記例を用いて整理します。
- シフトを作成するにあたり必要なことを把握する
- 人数はどれくらい必要か / いるのか
- どれくらい期間のシフトを考えるのか
- 時間労働なのか、裁量労働なのか
- 人員の形態を整理する
- 個人やチーム、グループで働く必要があるのか
- チームやグループに分けることは可能か
- どのようなグループにできそうか
- 能力や年齢、相性の良さでグループにする
- 新人とベテランでグループにする
- ランダムなグループにする
- 人員要望にはどのようなものがあるか整理する
- 要望のうち絶対叶えないルール
- なるべく叶えたいルール
勤務者でチームやグループを組むことでできれば、数理最適化問題のモデルとして起こす際にチームでの集合を定義する必要があります。また、新人には指導者が必ず必要であれば、そのチームの中に新人がいる場合はベテランは少なくとも一人いれるなどの対応(制約)ができそうです。
条件として考えたいことがあればあるほど、一般的には数理最適化問題は解くことが困難な問題へと近づく可能性があります(制約の種類にもよる)。そのため、制約として順位をつけておくことをおすすめします。そうすることで、問題の難易度をコントロールできる可能性があります(絶対守るべき制約が守れないことに最大のペナルティがかかるようにし、そのペナルティを最小にする目的の問題にするなどといった対応)。
目的の整理
次に目的としたいことを以下の例のように、一つ決めてみます。
- 一ヶ月の間でなるべくみなが同じ勤務回数(給料)になるような勤務表にしたい
- 勤務する人に回数のばらつきがないようにするため
- 個々で出したシフト希望の採用回数の差分が少ない勤務表にしたい
- Aさんだけシフト希望がたくさん通っているという現状を避けるため
- 休みの希望がなるべく通る勤務表にしたい
- シフトの希望より休みの希望をなるべく通してあげることで、人員の満足度をあげる
- 制約の違反度が少ない勤務表にしたい
- 制約がなるべく守れるような勤務表を作成することと同じ意味です
制約の整理
最後に制約を考えてみます。この際、絶対守るべき制約となるべく守りたい制約にわけることが可能ならチャレンジしてみてもいいかもしれません。
- 誰でも少なくとも週X回は勤務する
- 健康状態を損なう過度なシフト並びは禁止する
- 多くて連勤はX日まで
- 夜勤の次の日は朝勤務禁止にする
- 夜勤は週X回まで
- 休みはX回とる
- 新人がいる場合、必ずベテランが同じ時間帯に出勤する
おわりに
どうでしょうか、意外と情報として収集すること・考えておくべきことの量の多さに圧倒されませんか?
ここまでのような作業ができてようやく、数式などを用いて定式化することが見えてきます。ここからは、だんだんとハードルが高くなってきます。筆者の個人的な意見ですが、定式化をすんなり行えるようになるには、かなりの訓練が必要です。情報整理ができたら、まずは弊社のようなプロに相談して定式化できそうか依頼するのも一つの手ではないかと思います。(お問い合わせフォームよりお気軽にお問い合わせください)
スケジューリングを行うといっても、数理最適化を用いる以外に、GA(遺伝的アルゴリズム)やSA(アニーリング)を用いることもあります。今回は「はじめに」で紹介した4つステップのうち、1つ目を取り上げて説明しました。残り3つの要素について詳しく知りたい場合には是非「[最適化問題のすゝめ:第1部] 数理最適化とは?種類や特徴を解説 」や「第2部] 数理最適化の問題を解いて理解を深めよう 」をご覧ください。
次回更新もお楽しみに!
執筆者:山本


